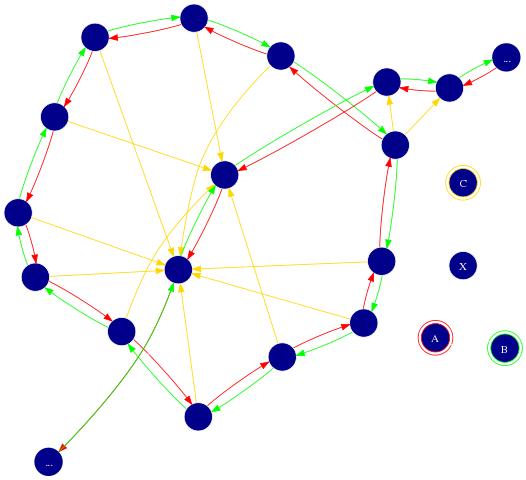
A closer look at the soup

Matt's soup from orbit:
- It's omnipresent
- It's omnitenerent (except possibly trans fats)
- ...and that's it.
Note that while no concepts were irrevocably harmed in preparation of this presentation it does contain egregious abuse of notation and graphic scenes of undefended asymptotes.
Coming closer

And closer

.

Better, but we're still not there yet.
Ah, here we are.

A brief refresher course
- Vectors have a geometric interpretation
- a⋅b = |a|⋅|b|⋅cos(θ) = Σai⋅bi
- a⋅a = |a|2 = square of the length
a×b = |a|⋅|b|⋅sin(θ)⋅(a unit vector perpendicular to both a and b)
- Meaningless for n < 3
- Coals to Newcastle for n > 3
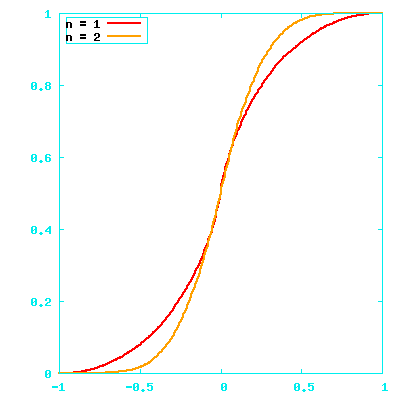
Integral of a distribution
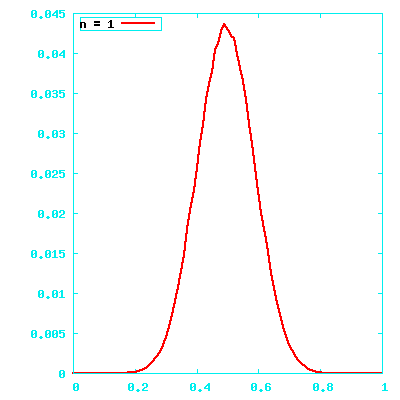
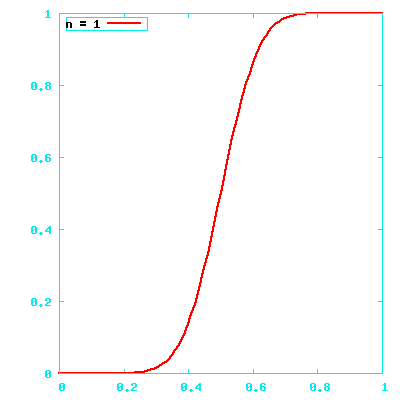
Start with simple vectors
- One element in the range -1.0..1.0
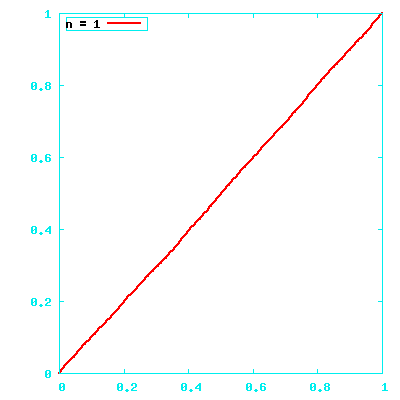
|a| will be uniformly distributed over 0.0..1.0
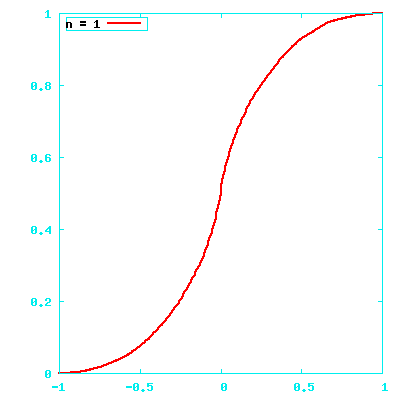
a⋅b/|a||b| ≈ 2⋅a⋅b
For two dimensions
- Two elements ∈ -1.0..1.0
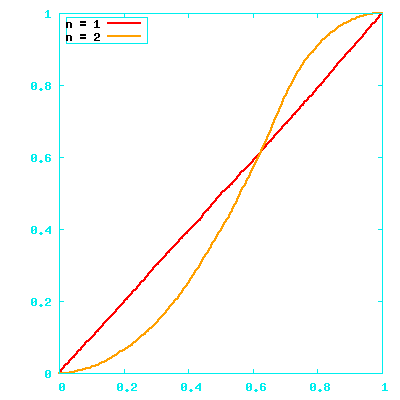 i
iThe ais making up |a| tend to average out.
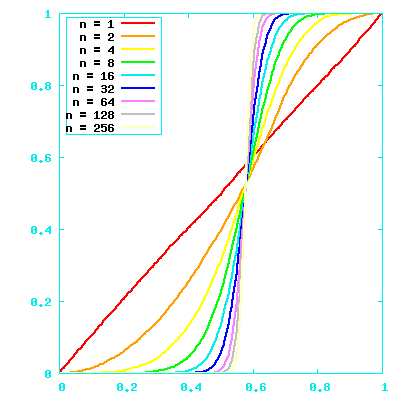
The ai⋅bi terms tend to cancel out
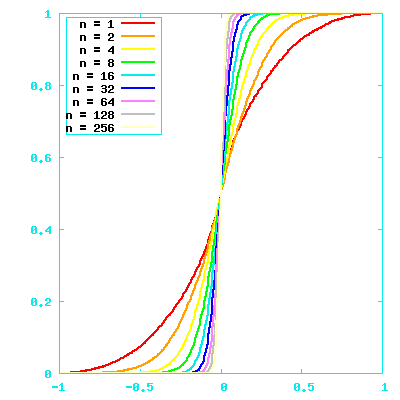
Lots of dimensions, values still in -1.0..1.0
|a| is generally pretty close to (√n)/2
a⋅b is generally pretty close to 0
Values in {-1,1}
- In one dimension, it's [1] or [-1]
- |a| is always 1
- a⋅b is 1 or -1
- In two, it's ∈ { [1,1], [1,-1], [-1,1], [-1,-1]}
- the corners of a square
- |a| is √2
- a⋅b/|a||b| = 1 for 1/4, 0 for 1/2, -1 for the other 1/4
- In general
- the corners of a hyper-cube
- |a| is √n in n dimensions
- The dot product will distribute as (k n)
Values ∈ {-1,1}, graphically
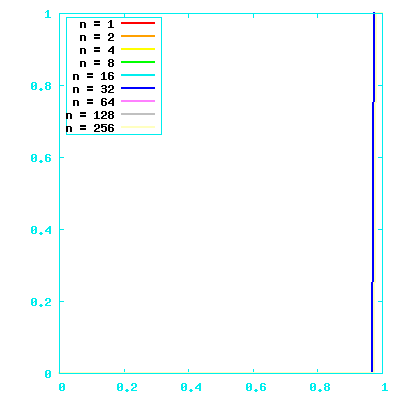
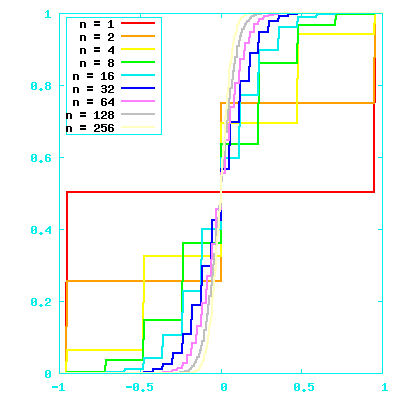
Values in {0,1}
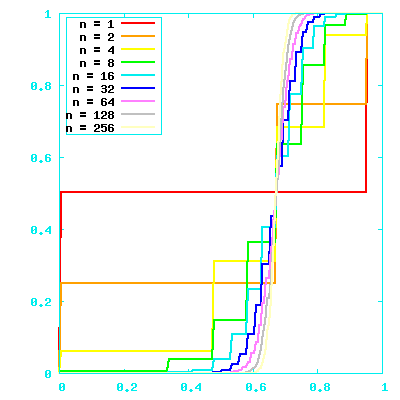
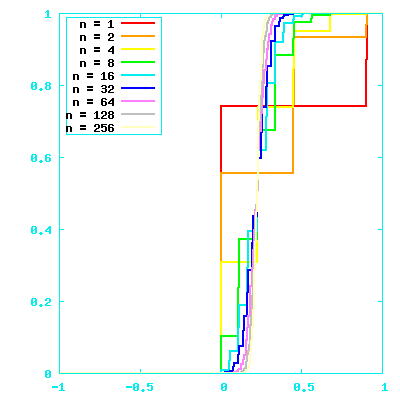
Values in {0,1}, with 1s rare compared to 0s
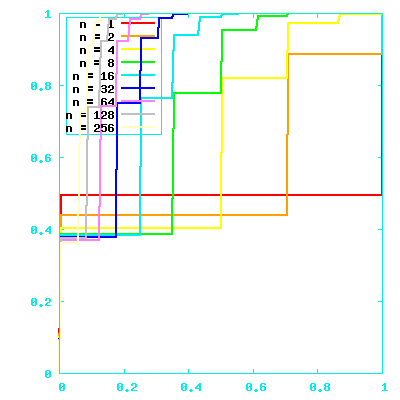
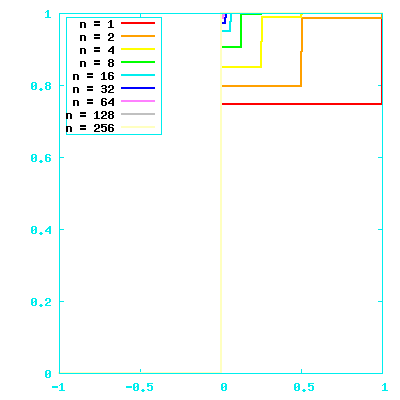
Shameless sweeping generalization
There are scads of other options
- {-1,0,1}
- {0,1,2,3,...255}
- {±1, ±1/2, ±1/3...}
- etc.
But when n gets large we pretty much always have:
- |a| ≈ some constant (most of the time)
- a⋅b ≈ 0 (most of the time)
So what could we do with these?
Or better, what couldn't we do with them?
- Write abstruse papers for obscure journals
- Wrap fish
- Quantum mechanics
- Use them as GUID (for G ≠ "Global")
- Waste memory
- Concoct goofy presentations
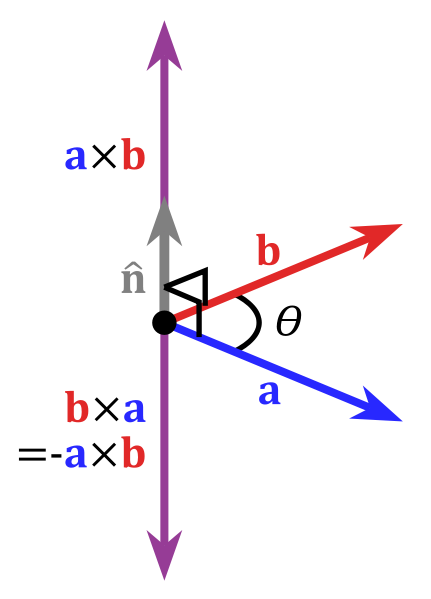
Fun cross product facts
- a×b = [ a2b3-a3b2, a3b1-a1b3, a1b2-a2b1 ]
- if a⋅ b = 0 and c = a×beta we can find c from a & b, b from a & c, and a from c & b
- Doesn't make sense except when n = 3
- Beyond quaternions
- If n is a multiple of 3 we can take the components in triples and write:
a×b = [
a2b3-a3b2, a3b1-a1b3, a1b2-a2b1,
a5b6-a6b5, a6b4-a4b6, a4b5-a5b6,
a8b9-a9b8, a9b6-a7b9, a7b8-a8b7,
:
]
Consider two object c and c'
- c' := c⋅(1-ε) + (a×b)⋅ε
- c' is pretty close to c ( c⋅c' ≈ |c|⋅|c'| )
Given c' and a we can probably get b back:
(c'×a)/ε = c⋅(1-ε)×a/ε + (a×b)×a ≈ 0 + b
One way to read this:
- c = an object
- a = a property name
- b = a value
- c' = "an object mostly just like c but if we ask it for something like a we'll get back something like b"
- c.a := b ⇒ c ← c⋅(1-ε) + (a×b)⋅ε
- c.a ⇒ (c'×a)/ε = c⋅(1-ε)×a/ε + (a×b)⋅×a
TNSTAAFL

But wait, there's less!
c.a := b
c.a := d
c.a ⇒ b ∪ d
Starting over with e instead of c, we could try:
e.a := b
e.a := ¬b (-1⋅ the vector representing b)
Key encoding
Instead of:
c.a := b ⇒ c ← c⋅(1-ε) + (a×b)⋅ε
we probably really want something like:
c.a := b ⇒ c ← c⋅(1-ε) + ((a×1k)×2b)⋅ε
Where ×1 and ×2 are cross-product analogues with different partitionings and k is an arbitrary vector.
This lets us distinguish c.a := b from c.b := a.
Other reasons to structure the keys
- We can code more information in the linkage; by using different "k"s we could distinguish things like:
- Keys
- Indexes
- Methods
- Instance variables
- By "scrambling" like this we can also deal with cases where the key (or value) is the object itself.
The null key encoding
So what does the null-encoding
c' = c⋅(1-ε) + b⋅ε
mean?
The a has dropped out entirely, and in general c' will have the same properties c had. Only on issues where c is mute will b have any impact.
Levels of interpretation
- Oth order: Color = (Red,Yellow,Blue)
- 1st order: struct { int x; int y; }
- 2nd order: javascript, anyone?
- Where next?
- Smalltalk/Ruby inheritance
- Matt's favorite, FSMs
- Extending ¬ to genera & difference
- Turtles all the way down
Relationships are objects
- A bare relationship is a triple {subject, role, value}
- But this is just a vector
The role component has inheritance
... relative ← ancestor ← grandparent ← grandmother ...
Relationships can be more structured (frames)
- [the sum of 1 and 2 is 3]
- Movie tropes
- Can be written as Prolog
- This is Matt's soup!
Skipping a few hours of material

Bootstrapping the soup
- Assign a random vector to each thought/concept/category
- Using the declared structure as a guide
- Iteratively adjust the vectors
- Stop when they represent the desired structure
Refinements
- Let them move a lot at first (large ε) and cool down as they converge
- Lock the structure eventually in with a small ε
- Or use the template to form standing waves
- Introduce thoughts incrementally and have old thoughts move more slowly
Final outcome is basically the same
What you get is a density function over a Hilbert space.

So where does that leave us?
- Spaces are composable
- Neighbors
- Lots of them:
- i = 1, n = 2, |{r ≤ i}| = 2
- rises roughly as in with some πs
- Very minor (but meaningful) differences
- Easy dot product circuit
- Find by pattern / unification / matching
- Analogues to modal reasoning models (temporal, counterfactual, intensional, provisional, etc.)
- Failure modes suggestively similar to known human mental failure modes.
Finding our way in the soup

What does this mean?

How about this?
But this, on the other hand:
One possibility
The other
We'll probably see things like this
And this